Biology

Wayfinding Wavefronts: Cellular Chemotaxis

by Gregg

Dr. Robert Insall’s presentation on Chemotaxis, a mechanism by which cells can navigate complex spaces by detecting and amplifying cellular gradients, inspired me to replicate some of his work.

The full talk can be found on YouTube, and I highly recommend watching it. My favorite parts were his visualizations of simulated cells navigating mazes by chemotaxis, and then the way his real-world cells solved the same mazes in a very similar way.

I mocked up a similar simulation, and played around with it to see if I could learn anything the video didn’t contain.

Graphical Abstract

Cells enter a maze that's full of a chemical messenger (RED) being produced on the left-hand side of the screen, and follow two simple rules: (i) turn in the direction of the greatest concentration of the chemical, and (ii) when near some of the chemical, eat some of it. These two rules allow the cells to quickly find a collective solution to the maze, by creating a gradient of the chemical that points them in the right direction.
When the cells don't degrade any of the attractant, they can't efficiently explore the maze--instead they end up turning in circles looking for the signal, which is saturated throughout the maze.
When the chemical diffuses only slowly, the cells have a much harder time finding their way to the source of the chemical, but still do eventually find the source

Method

The maze is modelled as a grid with three types of tiles: Sources of chemoattractant, Open space, and Walls. Each tile has some concentration of chemoattractant between 0% and 100%; Walls never have any, while Sources always are full of chemoattractant. 

The chemoattractant diffuses to neighboring cells with some rate D, and cells remove chemoattractant from the cell they’re currently in at a rate of R. 

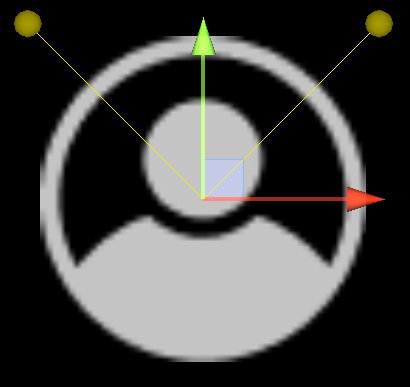
Cells are designed as described in the diagram below, and do three things each frame: (i) measure the concentration of chemical at each of their sensors (yellow spheres in the diagram below), (ii) turn towards the direction with higher chemical concentration, and (iii) destroy a fraction of the chemical present at their current location. 

The cellular model used for this study: cells are represented as circular objects that can collide with the world around them (and other cells). They face and move forward (green arrow), and sense the world using two sensors (yellow spheres) placed at 45 degrees on either side of the forward direction and at a fixed distance. The cells sense chemical concentrations at each of these two points, and then turn in the direction of the higher gradient at each time step.

Notes

This model of chemotaxis-driven navigation differs substantially from Insall’s model in many respects–primarily that it is less true to actual biological systems and less rigorously constructed. The model above does not feature a realistic model of diffusion–instead, a computationally cheap model was chosen. It does not feature realistic values for diffusion constants, cellular movement or turn rates, cellular sensing precision, nor cellular chemical destruction rates. 

Next Steps

  • Measure the number of cells that ‘solve’ the maze in fixed time as a function of the system parameters
  • Investigate application of chemotaxis to neural pathfinding