As part of research into the Gaia hypothesis and Earth System Science for a game Grow Together, I recently discovered Lynn Margulis and her pioneering work in symbiogenesis. I highly recommend reading this interview with her, as it covers some of her most important work and ideas in an understandable way, and sheds some light on her controversial character also.
In short, Margulis built off of the work of the 1900’s Russian biologists Mereschkowski and Kozo-Polyansky, and proposed that some cellular components, such as mitochondria and chloroplasts, are descended from free-living bacteria. The theory holds that long ago these bacteria entered a larger cell and formed a symbiotic relationship with the larger host cell, helping the host to survive in return for energy and a safe place to live. A large body of evidence has accumulated for this theory since Margulis and others began working on it. In this post, I’ll discuss one of the experiments that most surprised me, and I’ll then highlight parallels between Symbiogenesis and a recently-developed optimization framework called Combinatorial Learning.
Endosymbiosis in Amoebae
The most fascinating experiment I’ve read in symbiogenesic theory is K. W. Jeon’s work in symbiotic bacterial-amoebae relationships. While this work is very frustratingly not available for free online, the book “Symbiosis as a Source of Evolutionary Innovation: Speciation and Morphogenesis” (available for partial viewing here) contains a written summary of the results.
The experiment is as follows: first, infect a population of amoebae (referred to as D-amoeba as they are the D strain of Amoeba proteus) with a bacteria (called x-bacteria, because the bacteria is of unknown strain). The x-bacteria ends up killing a large number of the D-amoebae, but a few of the amoebae survive. The survivors end up living with the x-bacteria within their cell walls, and over the course of a few years develop a mutually dependent symbiotic relationship with the x-bacteria, such that any attempt to kill the x-bacteria (e.g. with antibiotics) ends up also killing the amoebae.
Once this mutually dependent relationship has formed, the amoeba are referred to as xD-amoeba, as they are morphologically distinct from the original symbiont-free amoeba. These xD-amoeba contain about 42,000 symbiotic bacteria per cell.
Here’s a visual description of the experiment, taken from wikipedia’s page on Symbiogenesis:
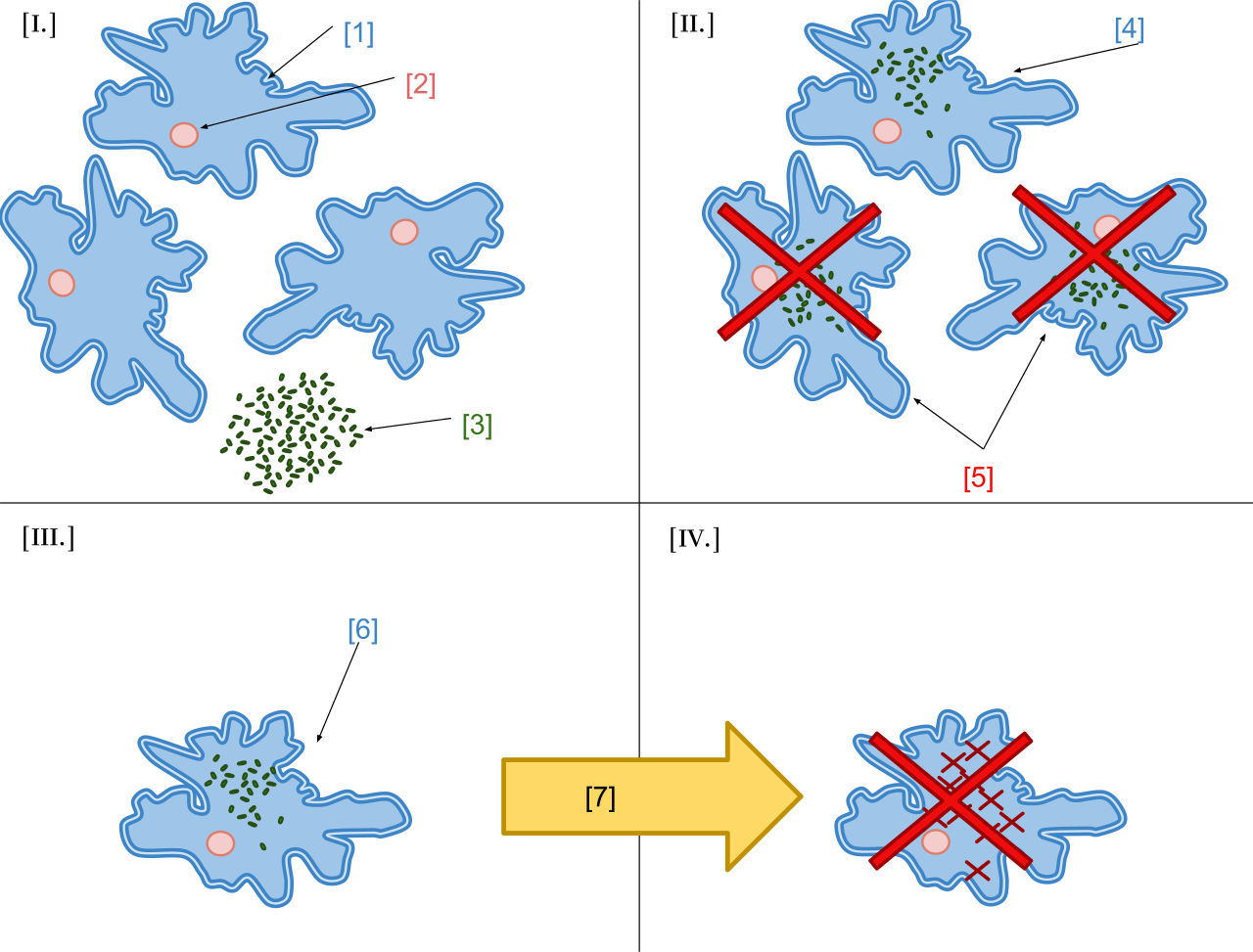
Interestingly, when the x-bacteria from the xD-amoebae are introduced to D-amoebae cultures (i.e. amoeba cultures that are unexposed to the x-bacteria), the D-amoebae quickly accept the x-bacteria, resulting in changes to their physiology. This demonstrates that over the course of the experiment the x-bacteria have evolved mechanisms to coexist symbiotically with D-amoebae, and that these mechanisms carry over to new populations of D-amoebae.
Beyond Biology
To me, this experiment is mind-blowing because it very simply highlights how symbiogensis can produce radically different organisms in short time scales through combination of distinct genetic sequences.
The concept of Symbiogenesis in biology is mechanically very similar to the concepts of Technological Parasitism and Combinatorial Evolution in complexity science. I’ll discuss the relationship that these two concepts have to symbiogenesis below.
Technological Parasitism
Technological Parasitism (Coccia and Watts, 2020) is the idea that parasite-host relationships evolve in predictable ways, and that technologies with a large number of parasites are counter-intuitively the most likely to evolve rapidly. While Coccia and Watts present this framework from the lens of technological development, it can also be applied to biological and artificial systems. In analyzing this framework, I’ll use “organism” interchangeably with “technology” to further the analogy.
The first essential argument of Technological Parasitism is that natural selection favors positive interactions between organisms: given an interaction between organisms, if that interaction can be modified to be more beneficial to one of the two organisms, it will be.
We can describe interactions between two organisms i and j using logical symbols (-, 0, +, ++), in increasing order of the positivity of the interaction, from negative to very positve. So, a relationship could be described as competition (-,-), amensalism (0, -), predation or parasitism (-, +), commensalism (+, 0), mutualism (+, +), or symbiosis (++, ++). The matrix below shows these relationships, and highlights with bold arrows how selection is likely to change the relationships over time, becoming more mutualistic and symbiotic.

This matrix is especially interesting when used to analyze Jeon’s work on bacteria-amoeba symbiogenesis. At the start of Jeon’s experiment, the x-bacteria infected the D-amoeba, using it to reproduce, and often killing the D-ameoba in the process. This is a parasitic relationship (-, +) that serves the x-bacteria. The D-amoeba that survived this infection were able to turn this relationship into a weakly parasitic, or even commensalistic (0, +) relationship, because they were able to survive and thrive in the environment while the x-bacteria lived inside of them. Finally, over the course of years the D-amoeba adapted into xD-amoeba that relied heavily on the x-bacteria to survive, an example of a strongly symbiotic relationship.
So, we can see that this biological example of technological parasitism conforms to the predicted evolutionary trend of increasingly symbiotic relationship dynamics between interacting organisms.
Combinatorial Evolution
Combinatorial Evolution, as described in Arthur’s “The Evolution of Technology within a Simple Computer Model”, is a powerful algorithm technique that rapidly solves complex problems using novel combinations of known solutions to simple problems. I recommend reading this paper, which is brief and describes Arthur and Polak’s approach and results better than I can.
Arthur describes this approach as follows:
New technologies are constructed–put together–from technologies that already exist; these in turn offer themselves as building-block components for the creation of yet further new technologies. In this way technology (the collection of devices and methods available to society) builds itself out of itself.
Taken from Arthur and Polak’s “The Evolution of Technology within a Simple Computer Model”
This approach solves complex problems in remarkably short time, and at first approximation mimics the process of biological symbiogenesis: two technologies (the x-bacteria and D-amoeba) that solve known problems are selected at random and combined with some mutation. The resulting aggregate system is saved as a technology (survives and reproduces) if it solves any problem better than previous technologies.
The parallel between these two concepts is clearly not one-to-one, but the primary driver of novelty–combining two existing organisms or technologies, and selecting for the aggregate system’s performance–is the same. Symbiogenesis and technological parasitism may therefore prove to be useful analogies and biological analogues of Combinatorial Evolution, and may help to guide development of useful combinatorial algorithms.
Future Work
I’m working on an extension of Combinatorial Evolution for supervised learning domains, in which sets of nonlinear functions (neural networks) are combined and then re-optimized to solve novel problems (post forthcoming). In writing this post, it occurred to me that Symbiogenesis with subsequent development of mutualistic relationships is an interesting biological analogue to the random combination of nonlinear functions with subsequent optimization via backpropagation. It may be fruitful design this supervised combinatorial evolution algorithm with these concepts in mind.